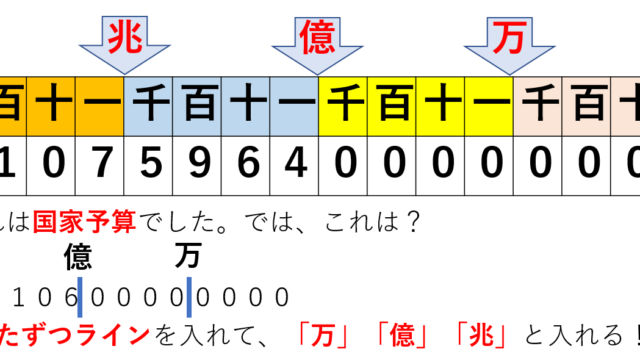
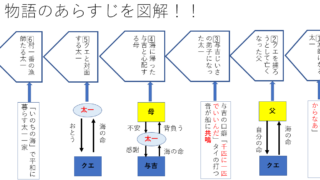
具象と抽象、帰納法と演繹法
1)具象と抽象
■論より証拠、以下の表を見てもらった方がわかりやすいかと思います。
| 具象 | 抽象 |
| クーラー、スイカ、アイスクリーム、氷 | 夏 |
| ぶどう、みかん、りんご、なし | 果物 |
この関係を認識させておくと、いろいろな理解が早いかと思います。そして、さらには、次の方法論(考え方)を与えておくのも重要なことかと思います。
2)帰納法と演繹法
| 帰納法 | 具象から抽象へと進む |
| 演繹法 | 抽象から具象へと進む |
例えば、国語科の説明文の授業を考えてみるといいです。
3)国語科では?
■説明文の構成を考える時、どちらからいったがいいかという問題です。最初から、三部構成に分けるのか、それとも各段落の要約をさせてから分けるのかということです。
| 帰納法でいく場合 | ・各段落の要約を具体的にやってみて、まとまりを見つけていく。 |
| 演繹法でいく場合 | ・接続語(まず、次に、最後に、ところで、さてなど)がはっきりしている時 ・問題文(=う。~か。)があって、最後に「こうして」や「このように」がある時 |
この方法論をもっておくと、子どもたちに指導しやすくなるかと思います。
4)算数科では?
■算数科で考えてみます。
例えば、台形の面積に関する授業シーンです。
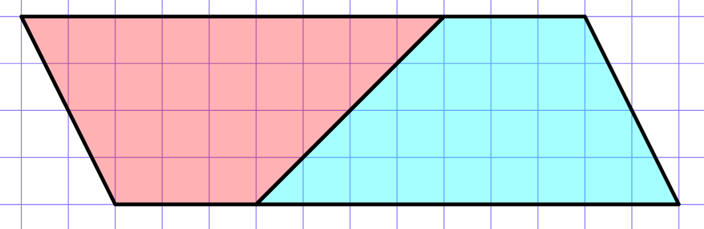
台形の公式を求めるのに、子どもたちにわかりやすい指導法は、次のように、具体的な台形について同じものを2枚逆転して重ねて提示するやり方です。
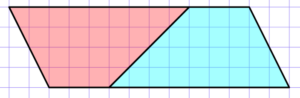
平行四辺形の公式は前の時間にやっているという前提です。そうなると、「底辺✕高さ」をすればいいことになります。つまり、
(3+9)✕4=48です。
しかし、2枚重ねているので、1枚分を求めるので、2で割るという必要があります。つまり、
(3+9)✕4÷2です。
この3にあたるのは、逆転した台形の上の長さ(上底)、そして9にあたるのは元の台形の底辺(下底)の長さとなります。よって、台形の公式は、
(上底+下底)✕高さ÷2となります。

この流れは、具象(例題)から抽象(公式)へと進む帰納法です。
そして、その公式を使って練習問題となっていきますよね。この場合は、公式を最初に使うので演繹法となりますね。
5)理科と社会科では?
■理科だと、どうなるでしょうか。
理科は何らかの「具体的」実験や観察を通して、法則(抽象概念)を導いていくという感じですよね。
社会科だと、具体的な写真やモノから気づきを出し合って、「仕組み」へとつなげていくことになります。つまり、社会科と同じですね。帰納法となります。他に、こんなシステムがないかなと考えていくことで、演繹法となりますね。
例えば、学校の屋上の貯水施設、一度電気ポンプを使って水を引き上げ、階下の水道蛇口へと重力(無料)で水を配置しくシステム、これは町中でも応用されていますね。その地域の小高い丘に貯水施設を作って、そこから各家庭へと配水していくパターン、これは同じですよね。
6)まとめ
■いつもこんな感じで、具象と抽象、やり方として帰納法と演繹法を頭に入れて授業構想を練っていくといい授業になってくるのではないでしょうか。